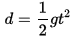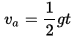If you are more comfortable with SI/metric measurements, this is generally not a problem.
4e mainly uses just yards and pounds, or units derived from these, so the only conversion numbers you need to remember are 0.914 and 2.2.
-
One hex can be considered to be either a yard or a metre with little actual effect on game mechanics unless larger numbers are involved.
For metres into yards divide by 0.914.
For yards into metres multiply by 0.914.
There are 1.094 yards in a metre. This can be treated as 1.1 and calculation made using the Times Eleven trick for metres into yards.
For an approximation of yards into metres, subtract 10% of the value from the number of yards.
A handy fact to remember is that 7 yards is about 6.4 metres.
-
An item's weight/mass in kilograms can be converted to pounds by multiplying by 2.2.
You can use the Times Eleven trick and double the result.
Divide by 2.2 for pounds into kilograms.
-
Tons in GURPS are “short tons” of 2,000 pounds or 907.185 kg.
Multiply metric tonnes (megagrams!) by 1.0231 to convert to short tons or divide by 0.907.
A useful visualization to remember is that a cubic metre of ice weighs nearly one metric tonne (919 kg actual).
A cubic yard of ice weighs 0.77 short tons.
-
Speeds in kilometres per hour can be converted to miles per hour by dividing by 1.6.
The mph result can then be halved to get the more game-useful yards/sec equivalent: 4 mph=2 yd/s.
Or, multiply km/h (kph) by 0.304 (or just 0.3) to convert directly into yd/s (0.303781 actual).
For kph to metres/s multiply by 0.2778 (0.277 ̇ actual) or divide by 4 for “quick and dirty”.)
Other US units used, such as cubic feet or cubic yards can usually be treated as arbitrary game units.
There are 27 cubic feet (cu.ft) in a cubic yard (cu.yd). A cubic yard is 0.765 cubic metres.
A cubic yard of ice weighs about 0.77 short tons, or 1,549 lbs. A short ton of water occupies 32 cubic feet.
Some parameters, such as jumping distances (p.B 352), are initially calculated in feet or inches. Divide by 3 (feet) or 36 (inches) to get yards.
A square yard is 9 square feet.
Cubic foot, cubic yard and square foot are abbreviated as cf, cy and sf in some GURPS publications.
Times Eleven Trick
Modified from “Rapid Math Tricks and Tips” by Edward H. Julius.
To multiply by 1.1 (metres into yards) write the original number then beneath it write the same number, with the decimal point shifted once to the left (ie, a tenth of the original number). Add these two numbers.
37 metres = 37 + 3.7 yards = 40.7 yards.
Note that subracting the smaller number from the larger gives you 90% of the original value. This gives you an approximate conversion of yards into metres.
85 yards = 85 – 8.5 metres = 76.5 metres.
To convert kilos into pounds, double the value in kilos and use the process above for the final result in pounds. Subtract 10% and halve for pounds into kilos.
5 kg = 10+1 lb = 11 lb
20 lb = 20 – 2 lb = 18 lb = 9 kg.
Temperature
Temperature can be a problem.
Many rules for GURPS are written referring to 10˚(F) increments, for example.
p.B9 tells us “one Fahrenheit degree is 5/9 the size of a degree Celsius” and “To convert actual thermometer readings, subtract 32 from the Fahrenheit temperature and multiply the result by 5/9”.
℉ = (℃ x 1.8) +32
℃ = (℉ – 32)/1.8
More convenient is to remember the approximation that for each degree of difference:
1℉ = 0.55℃
1℃ = 1.8℉
More easily remembered as:
10℉ = 5.5℃
20℉ = 11℃
18℉ = 10℃
Hence, when a rule talks of “for every 10˚ change in temperature” it can be read as “for every 5℃ change…”.
The comfort zone defined in Temperature Tolerance on p.B93 can be read as being: “For ordinary humans, this zone is 30℃ wide and falls between 1℃ and 32℃”.
See here for a different approach to GURPS and metric.
Hex Number and Area Formulae
In GURPS, and some other games, one often encounters statements such as “affects an area of x radius hexes”. Just how many hexes are in a x radius area? How many doses of drug, or pounds of cyberswarm, will you need to cover a given area?
The hexes on a hex-grid constitute a “centered hexagonal number” or “hex number”. The number enclosed by a given radius can be determined by the simple formula:
(r(r+1) x 0.5) x 6 + 1 or 3(r(r+1)) +1 = total area in hexes
Where “r” is the radius from the centre hex in hexes.
Put another way, the hex-number is one more than six-times the triangular number (see illustration below).
Remember to observe the BODMAS rule when using this formula or any other.
Solve the operations within brackets first, then perform multiplications before additions. For this particular formula this means adding 1 is the last thing you do.
Thus for a radius of two hexes: (2(2+1) x 0.5) x 6 + 1 = (2 x 3 x 0.5) x 6 + 1 = 3 x 6 +1 = 18 + 1 = 19 hexes area.
For quick reference, the progression of hex numbers is: 1, 7, 19, 37, 61, 91, 127, 169, 217, 271, 331, 397, 469, 547, 631, 721, 817, 919.
Space Travel Formulae
While on the subject of useful formulae and conversions, a useful one for Transhuman Space and other space-based campaigns is:
Delta-V (mps) ÷ 1100 = au/ day
or
Days of Travel = Distance in au/ (delta-V (mps) ÷ 1100)
Where “mps” is “miles per second”.
To convert Delta-V (mps) to a top speed in yards per second multiply by 1,800. (1,760 actual)
To convert Acceleration in G to a move of yards per second per second multiply by 10. (10.72 actual)
It is easier to deal in interplanetary distances in Astronomical Units (au) rather than millions of miles or kilometres.
An Astronomical Unit (au) is an unit of measurement approximate to the average distance from the Earth to the Sun.
For game purposes, one au is approximately 93 million miles, 150 million km, 500 light-seconds or 8⅓ light-minutes.
The speed of light is approximately 186,000 miles per second or 300,000 km/s. Therefore a light-second is approximately 186,000 miles, 300,000 km or 1/500th of an au.
Light-lag in seconds is distance in au multiplied by 500. Double this value for a two-way communication.
For simplicity, the travel distance between planets within a star system may be taken to be equal to the distance of the further planet from the star.
The closest two planets will be to each other will be when they are in “inferior conjunction”: i.e. when they are in a line on the same side of the star. In such a configuration the distance between them will be “A-B” where “A” is the distance of the further planet from the star and “B” is the distance that the inner planet is from the star.
The furthest distance between planets will be when they are in “superior conjunction”, each in a line on opposite sides of the star. The straight line distance between planets will be A+B in this case.
The average between “A+B” and “A-B” works out as just “A”, the distance of the outermost planet from the star.
For convenience and simplicity, the GM may decide to take the travel distance between two planets in a system to be the distance of the more outermost planet from the star.
THS 3e p.51 has a more accurate table of distances between Solar System planets for Jan 1st, 2100.
Falling Distances and Velocity Formulae
Page 431 (4e) of the basic rules gives a table of velocities for falling objects.
Alternately, the formulae below can be used using a value of 10.72 yards/sec2 for “g” on Earth.
For other planets, multiply this value by the relevant scaling factor (eg: 0.38 for Mars, 0.9 for Venus, 0.17 for Luna).
Increasing density of atmosphere or fluid the object is falling (or sinking) through will reduce velocity.
“t” is the time in seconds. “d” is the distance fallen in yards in “t” seconds. “vi” is velocity in yards per second after “t” seconds of falling.
“va” is the average velocity in yards per second for an object that has been falling “t” seconds.
The above do not consider air density, which would become significant during a long fall.
See quote below for fall distances to terminal velocity for people and objects.
A useful calculator that includes the effect of air densisty can be found here:
THS 3e p.57 notes:
Falling Damage: To compute falling damage under gravity other than 1 G. figure the damage that would have occurred under 1 G. per p. B131.[3e] then multiply it by the local gravity. E.g.. a fall that is computed to do 12 points of damage (before DR is taken into account) would do 24 points of damage under 2 Gs. but only 2 points under 0.16 G.
Falling Objects: Use a similar procedure for determining the damage done by falling objects. Those interested in absolute realism should be aware that terminal velocity (the maximum speed at which an object can fall before air resistance) is decreased in low gravity. More importantly terminal velocity is lower in a thick atmosphere, higher in a thin atmosphere and unlimited in vacuum! So the effective maximum fall (200 yards for most objects; 50 yards for people, who have high air resistance) may vary widely. A general formula: terminal velocity is multiplied by 0.25 in a very dense atmosphere (Venus), 0.5 in a dense atmosphere (Titan), 1.5 in a thin atmosphere (like some space colonies maintained at low pressure), and 2 in a very thin atmosphere (Mars). It is unlimited in trace atmosphere or in vacuum.